Cayley Graphs
Cayley Graphs are a way of representing groups. Let ![]() be a group with generating set
be a group with generating set ![]() . The Cayley Graph,
. The Cayley Graph, ![]() , is a graph where all members of
, is a graph where all members of ![]() are vertices, and two vertices,
are vertices, and two vertices, ![]() and
and ![]() , are adjacent if
, are adjacent if ![]() or
or ![]() for some
for some ![]() .
.
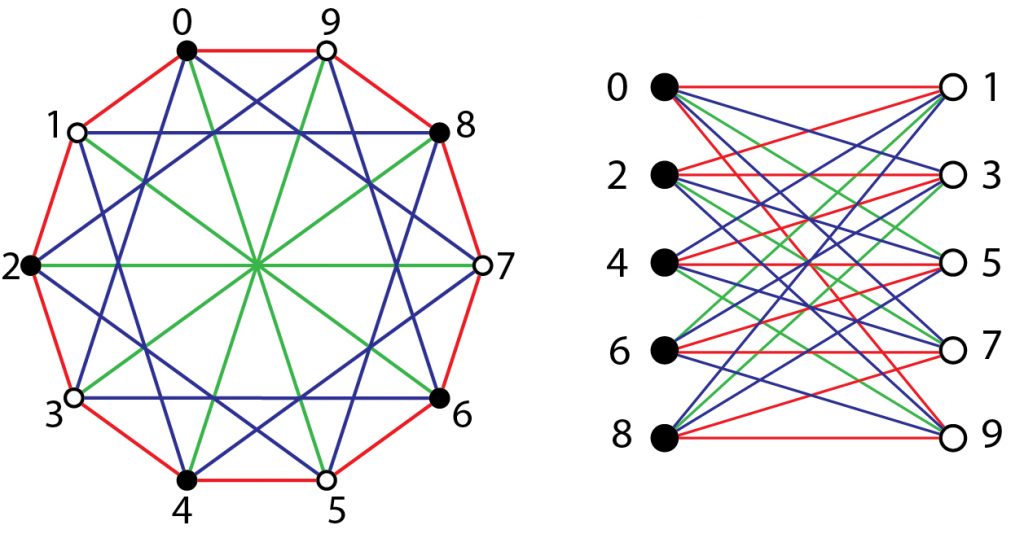
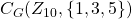 , drawn two ways. The red lines represent the vertices that are connected by the 1 in the generating set, the blue lines represent the vertices connected by the 3, and the green lines represent the vertices connected by the 5. Notice that
, drawn two ways. The red lines represent the vertices that are connected by the 1 in the generating set, the blue lines represent the vertices connected by the 3, and the green lines represent the vertices connected by the 5. Notice that 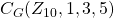 is the same as
is the same as 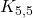 .
.Cayley Maps
Let ![]() be a closed generating set of
be a closed generating set of ![]() . The Cayley Map
. The Cayley Map ![]() is an embedding of
is an embedding of ![]() onto an orientable surface, where
onto an orientable surface, where ![]() is a rotation (cyclic permutation) of
is a rotation (cyclic permutation) of ![]() .
.
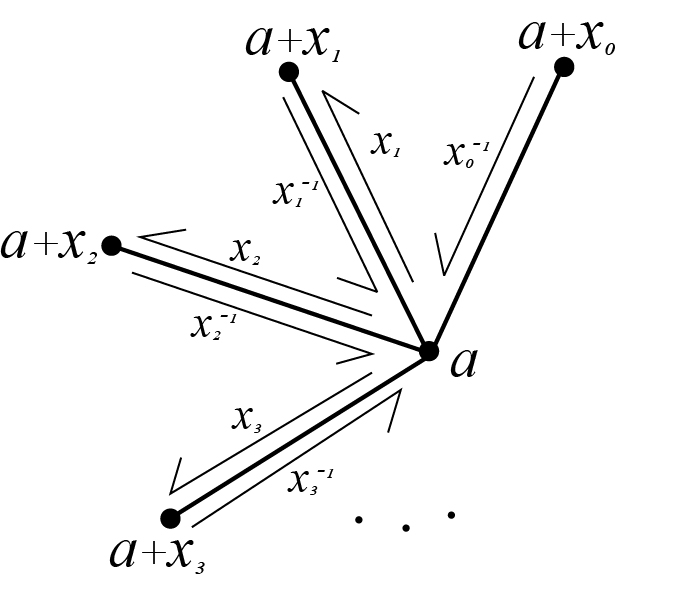
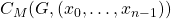 where
where 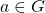 . Notice that the elements in the rotation are assigned to the branches of the Cayley Map in counterclockwise order
. Notice that the elements in the rotation are assigned to the branches of the Cayley Map in counterclockwise order