According to Ringel, the optimal genus for ![]() is
is ![]() . We were able to obtain the same genus using a Cayley Map with group
. We were able to obtain the same genus using a Cayley Map with group ![]() and rotation
and rotation ![]()
![]()

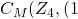
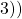
The face set is
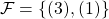 , where
, where 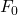 and
and 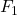 are both 4-gons. Using the Euler Characteristic Formula,
are both 4-gons. Using the Euler Characteristic Formula, 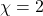 , so
, so 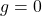 .
.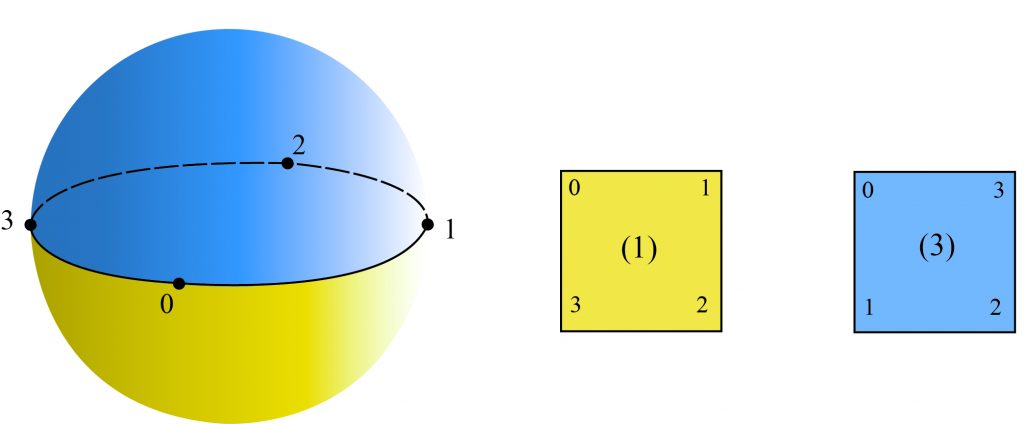
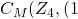
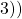 embedded into a sphere (
embedded into a sphere (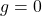 ). The blue square uses permutation
). The blue square uses permutation 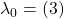 and forms the top half of the sphere, and the yellow square uses permutation
and forms the top half of the sphere, and the yellow square uses permutation 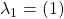 and forms the bottom half.
and forms the bottom half.Using the Dihedral Group ![]() yielded the same genus, but with one distinct face appearing twice. The reason for this difference is that each element in the rotation using
yielded the same genus, but with one distinct face appearing twice. The reason for this difference is that each element in the rotation using ![]() is followed by its inverse, whereas in the rotation for
is followed by its inverse, whereas in the rotation for ![]() , each element is its own inverse.
, each element is its own inverse.

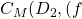 \hspace{1}
\hspace{1} 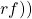 .
.The face set is
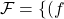 \hspace{1}
\hspace{1}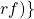 , where
, where 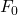 is two 4-gons. By the Euler Characteristic Formula,
is two 4-gons. By the Euler Characteristic Formula, 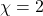 , so
, so 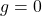 .
.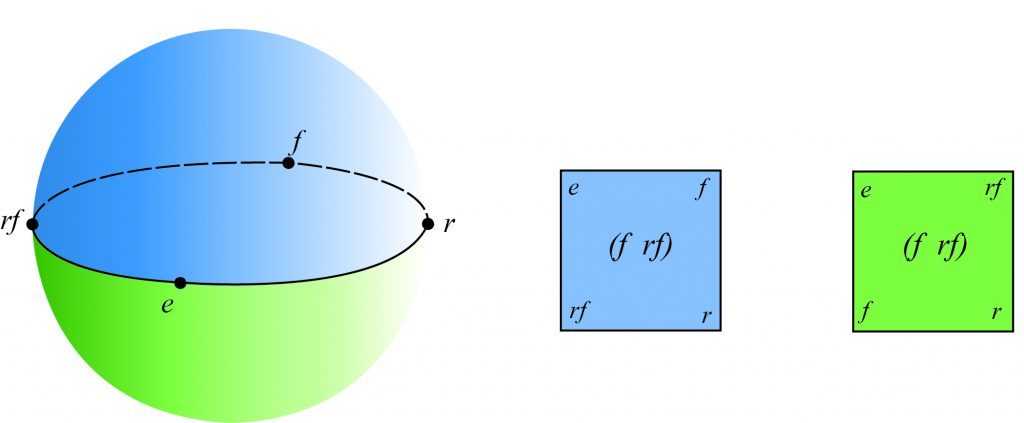
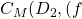
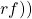 embedded into a sphere (
embedded into a sphere ( ). The blue and green squares use permutation
). The blue and green squares use permutation 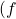
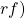 , and each face forms half the sphere.
, and each face forms half the sphere.