The optimal genus for ![]() is
is ![]() . We were able to obtain the same genus using a Cayley Map with group
. We were able to obtain the same genus using a Cayley Map with group ![]() and rotation
and rotation ![]()
![]()
![]() .
.
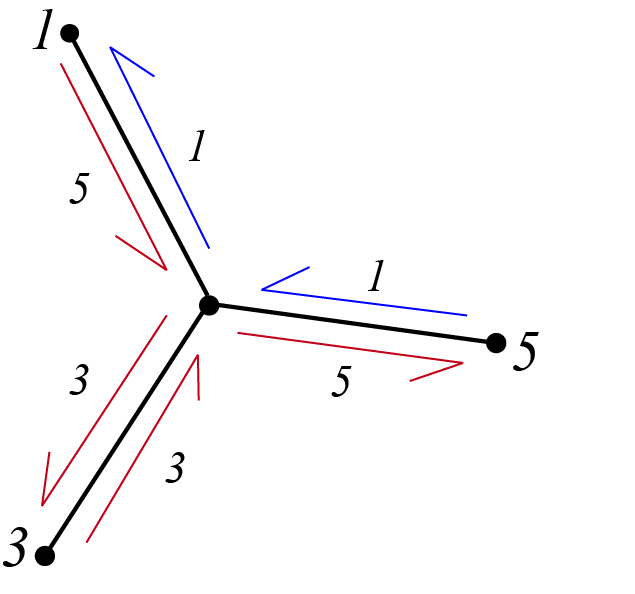
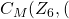 1 3 5
1 3 5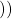
The face set is
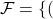 3 5
3 5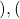 1
1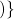 , where
, where 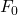 and
and 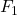 are both 6-gons, and there are two
are both 6-gons, and there are two  faces. Using the Euler Characteristic Formula,
faces. Using the Euler Characteristic Formula, 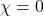 , so g=1.
, so g=1.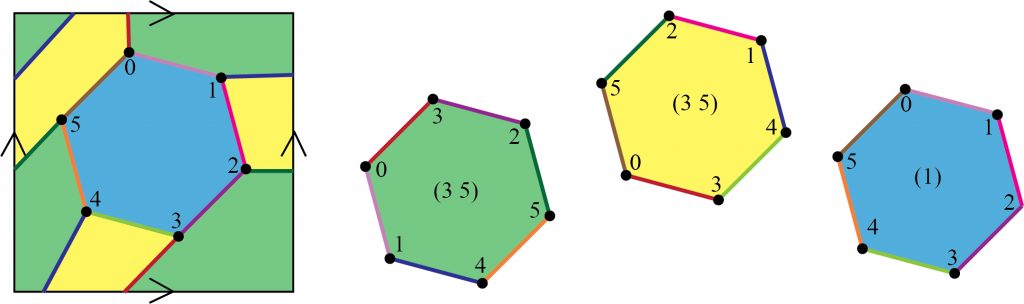
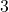
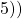 embedded into a torus (
embedded into a torus (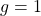 ). When the vertices are connected, the three hexagons (right) form a torus (left). The green and yellow faces use the permutation
). When the vertices are connected, the three hexagons (right) form a torus (left). The green and yellow faces use the permutation 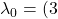
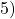 , and the blue face uses the permutation
, and the blue face uses the permutation 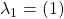 .
.
Because the rotation for ![]() only has three elements, there is only one other possible rotation,
only has three elements, there is only one other possible rotation, ![]() 1
1 ![]() . This rotation produces the same genus as
. This rotation produces the same genus as ![]()
![]()
![]() , but with different faces:
, but with different faces:
*** QuickLaTeX cannot compile formula:
\mathcal{F}={(3
*** Error message:
Missing } inserted.
leading text: $\mathcal{F}={(3$
*** QuickLaTeX cannot compile formula: 1),(5)} *** Error message: Extra }, or forgotten $. leading text: $1),(5)}. Using
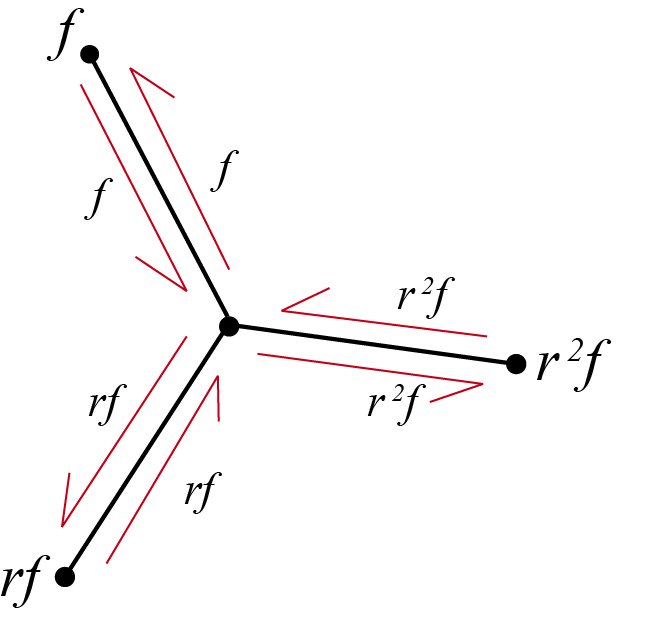
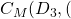 frfr^2f))\mathcal{F}=\{(f
frfr^2f))\mathcal{F}=\{(f*** QuickLaTeX cannot compile formula:
\hspace{1}
*** Error message:
Illegal unit of measure (pt inserted).
leading text: $\hspace{1}
rf*** QuickLaTeX cannot compile formula:
\hspace{1}
*** Error message:
Illegal unit of measure (pt inserted).
leading text: $\hspace{1}
r^2f)\}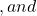 \lambda_0
\lambda_0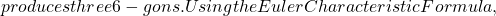 \chi=0
\chi=0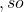 g=1$.
g=1$.