Rotations
Each vertex in a Cayley Map has the same rotation. That is, the graph is embedded on a surface such that the edge labels of the darts branching from each vertex are equal to the product (*) of the value of the vertex, ![]() , and each element in
, and each element in ![]() . The figure below shows the Cayley Maps for
. The figure below shows the Cayley Maps for
*** QuickLaTeX cannot compile formula:
C_M(Z_{6},(1 \hspace{2} 3\hspace{2} 5\hspace{2}))
*** Error message:
Illegal unit of measure (pt inserted).
leading text: $C_M(Z_{6},(1 \hspace{2}
, where each of vertices are a member of *** QuickLaTeX cannot compile formula:
(1 \hspace{2} 3\hspace{2} 5\hspace{2})
*** Error message:
Illegal unit of measure (pt inserted).
leading text: $(1 \hspace{2}
. \textit{Note: The remaining figures of Cayley Maps in this paper will show only the Cayley Map with center vertex 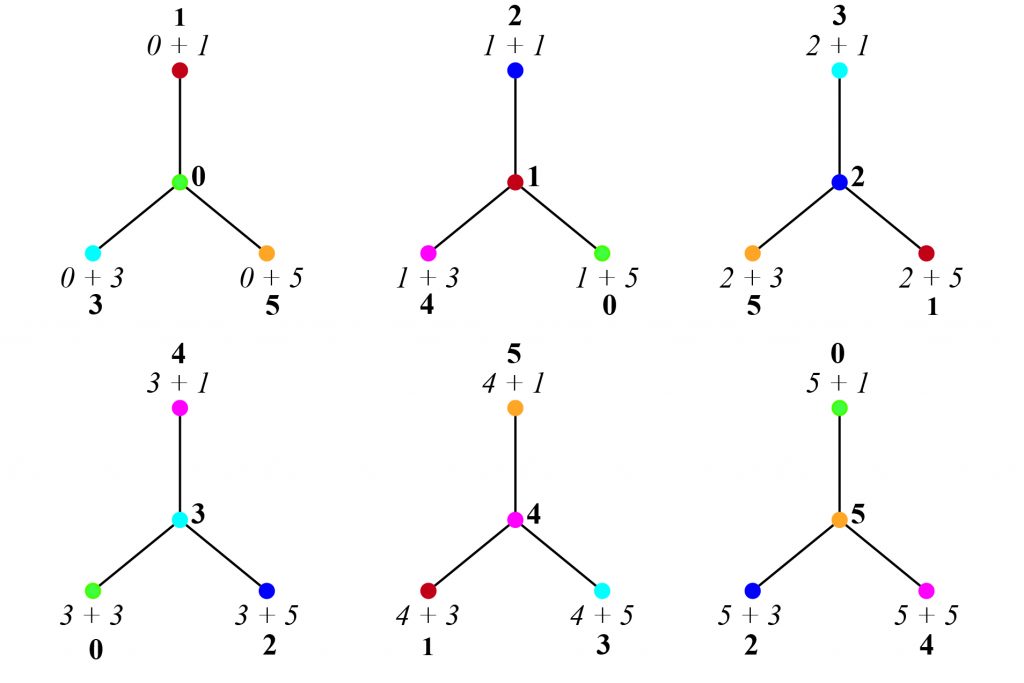
*** QuickLaTeX cannot compile formula:
C_M(Z_{6},(1 \hspace{2} 3\hspace{2} 5\hspace{2}))
*** Error message:
Illegal unit of measure (pt inserted).
leading text: $C_M(Z_{6},(1 \hspace{2}
for all vertices  .
.![]() – Suppose
– Suppose ![]() is a closed generating set for
is a closed generating set for ![]() , and
, and ![]() is a Cayley Graph for
is a Cayley Graph for ![]() . The only subgroup in
. The only subgroup in ![]() with order
with order ![]() is the set of even numbers
is the set of even numbers ![]() . Therefore, the coset of
. Therefore, the coset of ![]() , and thus the rotation of
, and thus the rotation of ![]() , is comprised of all odd numbers
, is comprised of all odd numbers ![]() .
.
![]() – Suppose
– Suppose ![]() is a closed generating set for
is a closed generating set for ![]() , and
, and ![]() is a Cayley Graph for
is a Cayley Graph for ![]() . Since the only subgroup of order
. Since the only subgroup of order ![]() in
in ![]() is the set of rotations, the coset of
is the set of rotations, the coset of ![]() is the set of reflections. Therefore,
is the set of reflections. Therefore, ![]() . Because reflections have order 2, every element in the rotation is of order 2.
. Because reflections have order 2, every element in the rotation is of order 2.
Faces
Connecting all the vertices of the Cayley Maps makes a mapping that forms a surface. The surface is comprised of faces. ![]() is the set of all faces formed by
is the set of all faces formed by ![]() .
.
Given a Cayley Map ![]() , where
, where ![]() is a cyclic permutation of a closed generating set
is a cyclic permutation of a closed generating set
*** QuickLaTeX cannot compile formula:
S^'
*** Error message:
Missing { inserted.
leading text: $S^'
, and *** QuickLaTeX cannot compile formula:
S^'
*** Error message:
Missing { inserted.
leading text: $S^'
defined by *** QuickLaTeX cannot compile formula:
C_M(Z_{10},(1 \hspace{2} 7\hspace{2} 5\hspace{2} 3 \hspace{2} 9))
*** Error message:
Illegal unit of measure (pt inserted).
leading text: $C_M(Z_{10},(1 \hspace{2}
.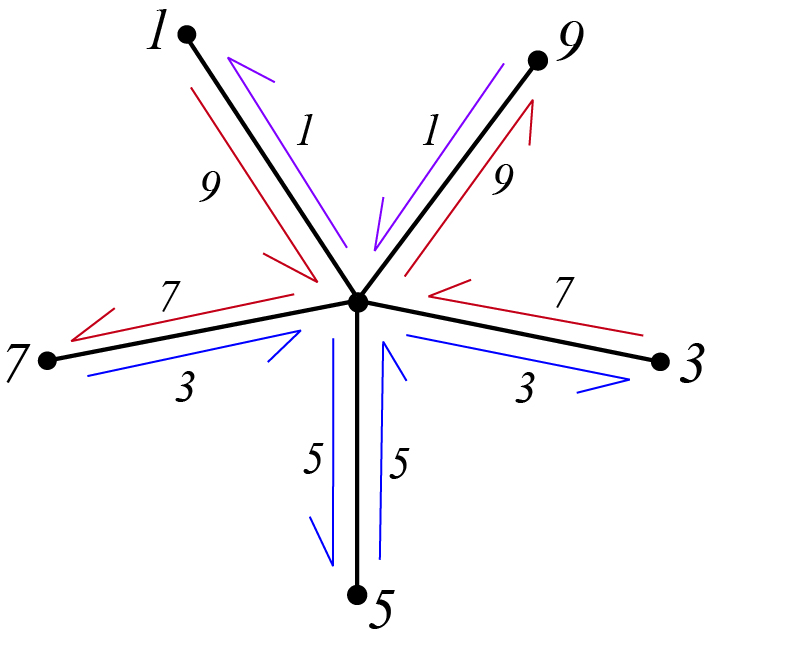
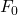 , the blue darts show the formation of
, the blue darts show the formation of 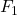 , and the purple darts show the formation of
, and the purple darts show the formation of 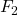 .
.
Equation 1. For each ![]() ,
, ![]() .
.
Explanation. In Figure 3, each branch of the Cayley Map is labeled with an element in the rotation, ![]() . An arrow pointing inward is labeled with the inverse (for instance,
. An arrow pointing inward is labeled with the inverse (for instance, ![]() ) of that branch’s element (
) of that branch’s element (![]() ). The following arrow, which points outward, is labeled with the next element in the rotation (
). The following arrow, which points outward, is labeled with the next element in the rotation (![]() ). These two arrows form part of a face (
). These two arrows form part of a face (![]() . Thus, the relationship between the rotation and faces can be described by the equation
. Thus, the relationship between the rotation and faces can be described by the equation ![]() .
.
More definitions and equations:
(a) ![]() is the face corresponding to
is the face corresponding to ![]() .
.
(b) ![]() is the length of
is the length of ![]() .
.
(c) If ![]()
![]() , then
, then ![]() is the order in
is the order in ![]() of the product
of the product ![]() .
.
(d) ![]() is the number of edges in the face
is the number of edges in the face ![]() .
.
(e) ![]() is the number of
is the number of ![]() faces.
faces.
(f) ![]() is the total number of darts in the embedding (twice the number of edges), where
is the total number of darts in the embedding (twice the number of edges), where ![]() is the number of vertices.
is the number of vertices.
\end{enumerate}
The example below shows the faces formed by ![]()
![]()
![]()
![]()
![]()
![]()
![]() , including the faces’ sizes and number of occurrences. \cite{citation4}\cite{citation5}
, including the faces’ sizes and number of occurrences. \cite{citation4}\cite{citation5}
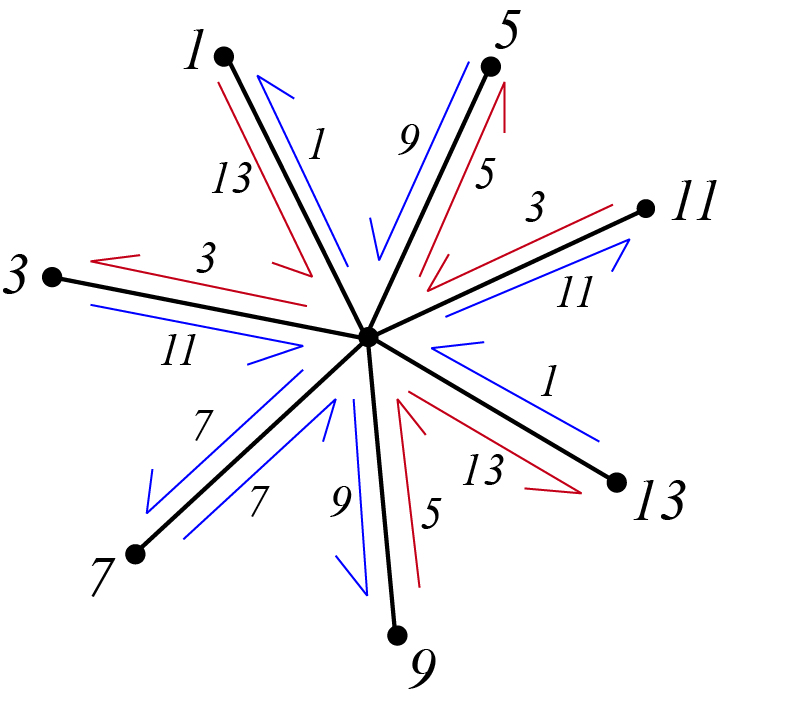
Example:![]() 5 1 3 7 9 13 11
5 1 3 7 9 13 11![]() is shown on the left.
is shown on the left.
Set of faces: ![]() 1 11 7 9
1 11 7 9![]() 5 13 3
5 13 3![]()
![]() 1 11 7 9
1 11 7 9![]() , is a 4-gon with four elements. Therefore, there are
, is a 4-gon with four elements. Therefore, there are ![]()
![]() faces.
faces. ![]() 5 13 3
5 13 3![]() , is a 6-gon with three unique elements. Therefore, there are
, is a 6-gon with three unique elements. Therefore, there are ![]()
![]() faces.
faces.
Finding Faces
To determine the minimum genera that the Cayley Maps could yield, we focused on face types rather than specific rotations. Though the faces that a Cayley Map forms depends on what rotation is used (Equation 1), identifying the specific type of faces (4-gon, 6-gon, etc.) that a Cayley Map can form does not require a specific rotation. One technique we used was ensuring there were elements in the rotation such that the product of the edges of a given face type would equal the identity of the group. For example, let ![]() be a Cayley Map of a particular complete bipartite graph that uses a specific group
be a Cayley Map of a particular complete bipartite graph that uses a specific group ![]() and some rotation
and some rotation ![]() , such that there exists a 4-gon
, such that there exists a 4-gon ![]() . There must exist either
. There must exist either
\begin{addmargin}[3 em]{3 em}
- Four elements in
 whose product equals
whose product equals 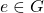 (i.e.,
(i.e., 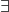
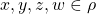 :
: 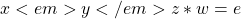 ), or \
), or \ - Two elements in
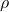 whose product squared equals
whose product squared equals 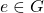 (i.e.,
(i.e., 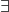
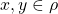 :
: 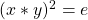 ).
).
\end{addmargin}
By finding whether or not such elements exist for a variety of face types, we were able to determine which faces could be formed by the Cayley Maps of specific complete bipartite graphs. After finding the smallest face sizes the Cayley Maps could form, we were able to determine the maximum number of said faces by using the equations described in Section 2.4.2 (d) and (e). The Euler Characteristic formula was then used to find the minimum genera for the complete bipartite graphs using Cayley Maps.